Geometria Fractal

Já pensou que retas paralelas podem se encontrar?

Quando aprendemos tipos de imagem, no design gráfico, duas representações gráficas costumam ser estudadas: A matricial, que consiste em um mosaico de pontos muito próximos, compondo uma imagem, e a imagem vetorial, que são equações que geram pontos (âncoras), que são ligados através de retas e curvas, em um plano, usando geometria cartesiana. Todavia, há uma outra forma de representar a imagem de forma computacional, uma forma pouco estudada em cursos de design gráfico, mas bem conhecida por quem trabalha com computação gráfica: a Imagem Fractal.

A Geometria Fractal descreve fenômenos da natureza de forma mais exata. As formas, na verdade, não são elementos geométricos montados. Árvores não são cilindros, com outros cilindros e cones, núvens não são círculos, girassóis não são estrelas, mas sim, como é definido pelo termo fractal, são “Objetos que apresentam auto-semelhança e complexidade infinita” (CONCI & AZEVEDO), ou seja, é a repetição eterna de cópias muito aproximadas de si mesmo.

Descrevendo de forma mais simples, imagine uma onda no mar. A onda é feito de ondas menores que, por sua vez, são feitas de ondas menores. Assim como a nervura de uma folha, que se estende para nervuras menores e para outras nervuras menores ainda.

Em 1854, o matemático alemão Bernhard Riemann descreveu o fenômeno de longitude e latitude com a afirmação de que linhas paralelas se encontram em um ponto: no polo.

A descrição de Riemann leva a uma compreensão diferente, porém lógica, do universo. A forma como vivemos deixa claro não haver necessariamente um plano reto, mas sim, que tudo possui uma curvatura.

Benoît Mandelbrot, em 1975, criou o termo fractal, baseado na interpretação de diversos trabalhos pelo mundo, que, diferente da geometria euclidiana resumida a 3 dimensões, mostra que é possível fracionar uma dimensão. Através do estudo de Mandelbrot, conclui-se que as paisagens terrestres possuem uma dimensão que ronda a “2.1”. Essa dimensão fracionada define o quanto a paisagem é irregular, o que mudaria de planeta para planeta.

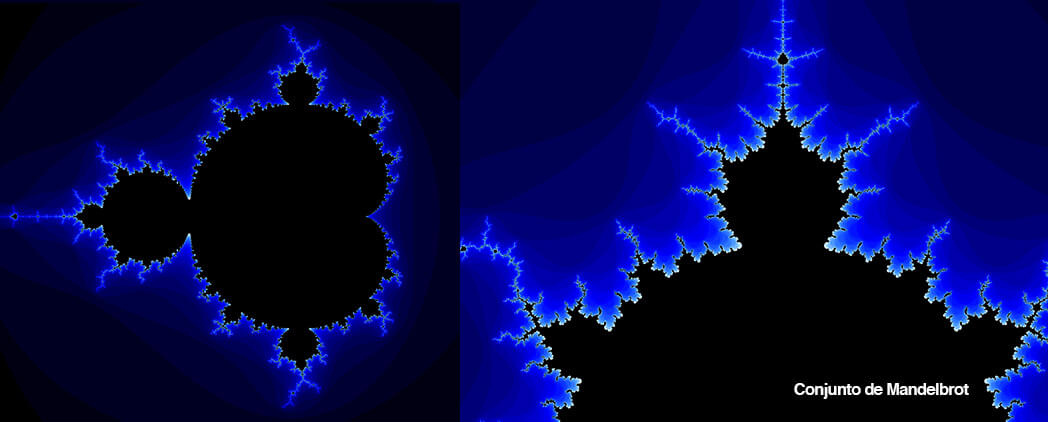
O conjunto de Mandelbrolt e o Floco de Neve de Kock são exemplos de fractais. Hoje a simulação do fractal para uso da computação gráfica baseia-se nesses exemplos, onde é adicionado um fator aleatório para poder aumentar a irregularidade da forma. Montanhas, oceanos e lagos, nuvens, etc. são criados a partir de fractais. A lógica que leva a reconstrução tridimensional de um fractal possui várias aplicações nos ramos da medicina, engenharia, meteorologia, dentre outros, incluindo, claro, o design.

A Sequência de Fibonacci

Anos antes da definição de fractal, matemáticos já se impressionavam com os padrões geométricos do que era natural, da forma como as conchas e samambaias se desenvolviam. É possível ver um padrão des semelhança em praticamente tudo o que é natural. Leonardo Fibonacci (1180-1250) sugeriu que seria impossível “subsistir algo se não for devidamente proporcional à sua necessidade”. Ou seja, que tudo precisaria de uma proporção, relativa ao que este é.

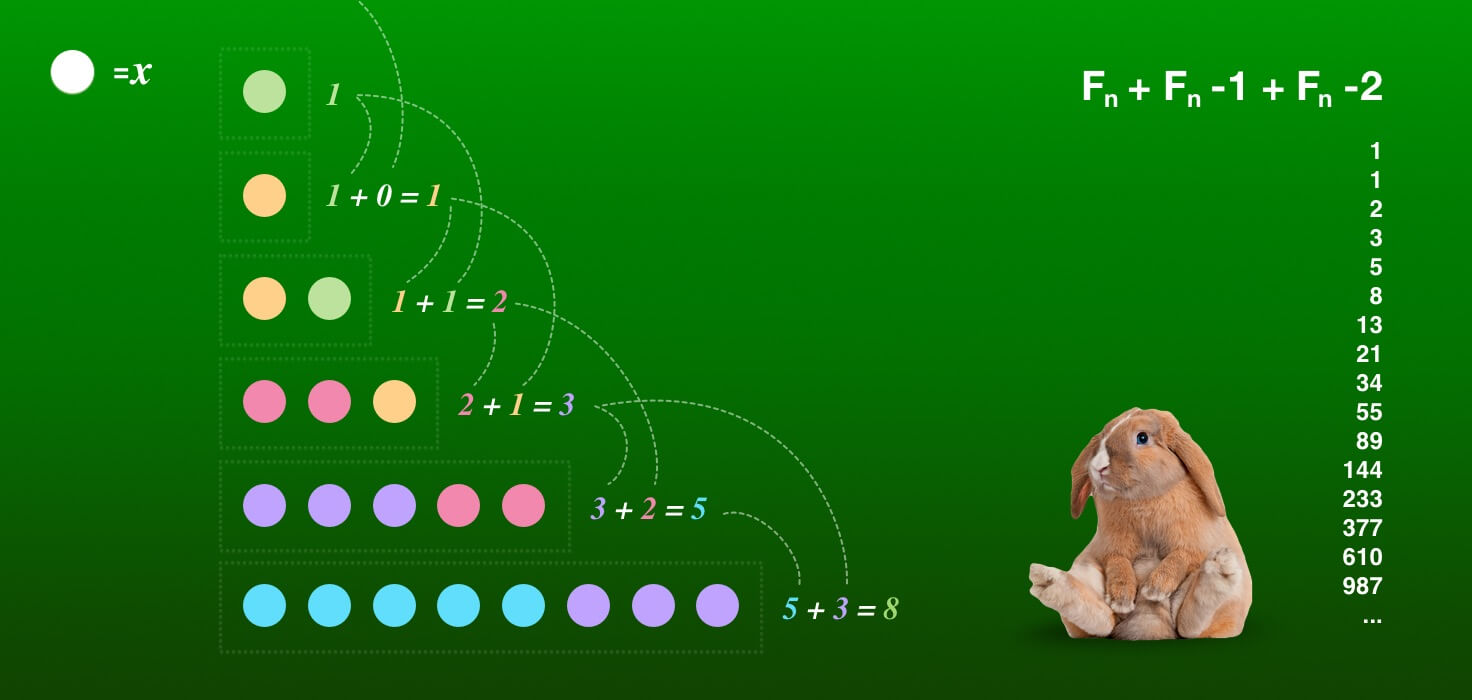
Sugerindo o problema da reprodução de coelhos, Fibonacci conseguiu definir uma sequência proporcional nomeada como Sequência de Fibonnacci.

Fibonacci sugeriu o problema dos Coelhos: Um casal de coelhos atingem a maturidade sexual em dois meses, a cada mês, um casal com maturidade sexual gera um novo casal. Considerando que as condições de reprodução desses coelhos sejam iguais, e ignorando qualquer problema genético, quantos coelhos teremos em N meses?

A resposta e dada pela sequência, considerando cada mês e quantidade de casais, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…

A sequência de Fibonacci é uma referência a um padrão matemático proporcional, isto é, o numeral 1 equivale a uma variável, é uma representação de algo. Essa sequência se baseia que o número atual seja a soma dos dois números anteriores. Matematicamente representado por Fn = Fn-1+Fn-2, em um processo de recorrência.

A representação do Fibonacci em um fórmula fechada, é representada pela equação abaixo:

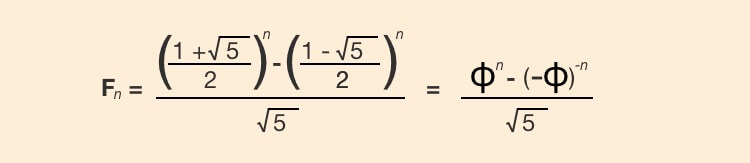
Um modelo muito comum e geometricamente eficiente de demonstrar a sequência de Fibonacci é através do Triângulo de Pascal. O triângulo de pascal segue uma lógica recursiva, similar a de Fibonacci, onde se demonstra algumas propriedades dos números binomiais. Gerado a partir de cálculos simples, mas trabalhosos, uma notável característica que se assemelha a descrição de Fibonacci pode ser encontrada. A de que o número atual é o produto da soma do número acima e de sua diagonal. Ou seja:

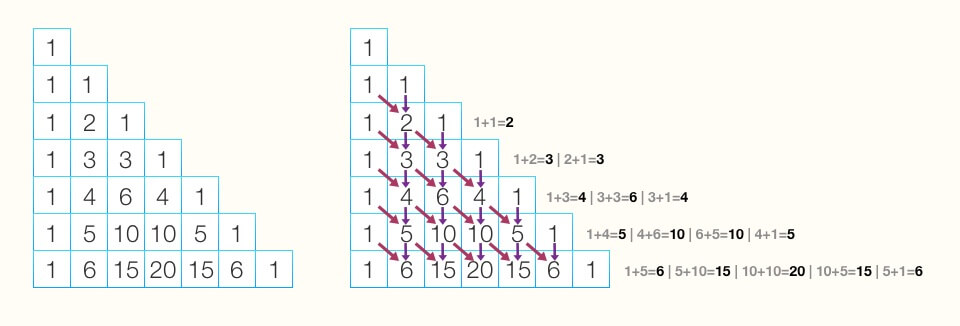
Esse é um comportamento bem interessante, mas onde está a relação com a sequência de Fibonacci? Com uma rápida olhada, não é possível visualizar, mas quando presta-se bastante atenção é possível ver a sequência de Fibonacci ao observar suas diagonais ascendentes.

A Sequência de Fibonacci descreve como as coisas podem crescer através da geometria fractal. Exemplos de como essa disposição numérica ocorre podem ser vistos em diversos elementos naturais, como as escamas de um peixe, o centro de um girassol, os flocos de neve e até mesmo a forma como as cores se formam na natureza. Para utilizar essa sequência, podemos obter a razão dela dividindo o número atual (n) com o número anterior da sequência e, a partir do terceiro número, vamos notar que há um certo padrão na divisão que se aproxima muito de um número bem interessante.

Quanto maior o número da Sequência de Fibonacci em razão ao número anterior, é possível encontrar um número aproximado e cada vez mais próximo ao número de ouro, φ.

O Número de Ouro

Os gregos antigos eram amantes das formas. Na busca pela Physis, pelo belo, pelo sentido, em sua arquitetura, em suas esculturas e em várias formas de manifestação artística, buscavam encontrar padrões matemáticos. O pensamento do cidadão grego se fazia forte na racionalidade e a compreensão de fenômenos naturais para dar um sentido as coisas, dar um sentido ao mundo.

Os gregos estudavam as proporções da natureza a partir de observações em imagens e sensações. A partir de um instrumento experimental chamado monocórdio, Pitágoras elaborou a escala musical usando como base uma proporção dois por um.  Essa proporção musical foi notada a partir da forma como a corda vibrava, se dividindo em seções menores, agradáveis, similares, porém em tons mais agudos.

Essa mesma proporção foi observada em uma forma geométrica em especial: o pentagrama regular, utilizado como símbolo principal da sociedade Pitagórica e existente em vários exemplos na natureza. O pentagrama foi escolhido por suas peculiaridades exatas.

O Pentagrama regular é obtido através das extensões das diagonais de um pentágono regular. Ou seja, como se as linhas do pentágono fosse esticadas até o momento que se encontram.

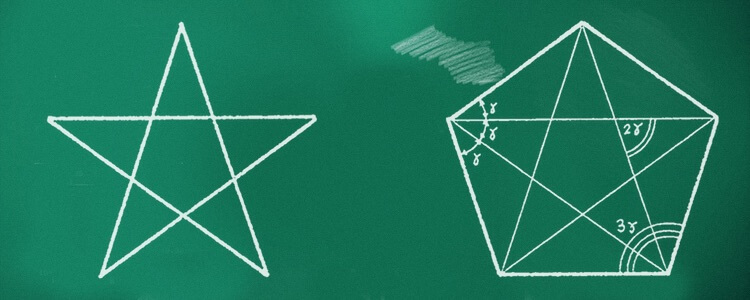
O que faz do Pentagrama algo realmente interessante é que a soma do comprimento das duas linhas mais curtas é igual ao comprimento da terceira linha, e a segunda e a terceiras linhas menores somadas são exatamente iguais a quarta. Essa característica foi chamada de Regra de Ouro, que gera a definição do que hoje é conhecido como Proporção Áurea.

A Proporção Áurea origina-se por uma razão recursiva específica de suas medidas e pode ser produzida infinitamente, descrevendo assim a natureza. Produz geometricamente o que talvez seja a forma básica mais usada nas artes: O Retângulo Áureo.

O Retângulo de Ouro pode ser gerado ao infinito mantendo sempre a mesma proporção. Essa geração infinita gera o que é conhecido como a Espiral de Ouro (ou Espiral de Fibonacci), tendo este nome porque a base da Proporção Áurea segue a mesma lógica da Sequência de Fibonacci.

A Geometria Euclidiana então sugeriu o que seria conhecido como retângulo perfeito que é gerado a partir da divisão em média e extrema razão. Pode ser definido então como quando “a razão entre as medidas de comprimento do lado maior e do lado menor é um valor aproximado do número de ouro”. Mas como obter um Retângulo Áureo?

Imagine um quadro perfeito. Agora encontre o centro de um dos lados. Você vai notar que o resultado é a divisão desse quadrado em 3 triângulos, sendo dois deles triângulos retângulos. Usando como raio a hipotenusa de um dos triângulos retângulos criados, e como centro de um cículo a metade do lado, podemos traçar uma curva que vai da outra extremidade da hipotenusa até a linha do centro do círculo. Completando as retas do quadrado até que se cruzem, é possível obter o que vem a ser conhecido como Retângulo Áureo, que leva esse nome por possuir as mesmas proporções que chegou as notas musicais e ao Pentagrama regular, ou seja, Possui a mesma Proporção Áurea.

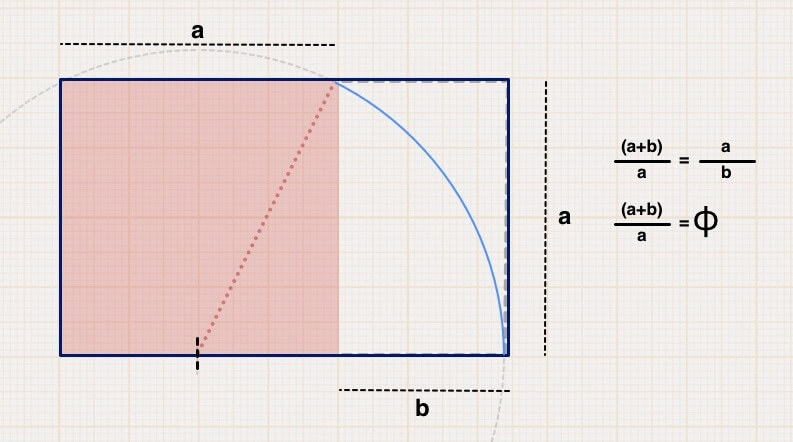
Mas afinal, qual é o valor algébrico dessa Proporção Áurea?

Com o Retângulo Áureo, podemos perceber que a razão entre seus lados é igual a seu lado menor dividido pela subtração de seu lado maior pelo seu lado menor. Vamos considerar que o lado maior seja L e o lado menor seja X. Considerando que L=1 teremos 1/x = x/1(1-x), o que nos resulta em uma equação do segundo grau, escrita como x² + x – 1 = 0. Aplicando Bhaskara, podemos chegar ao valor negativo de -0.6180… e o positivo de 1.6180…, como proporções são consideradas apenas positivos, obtemos a Proporção Áurea, ou o Número de Ouro, conhecido como Phi, conclui-se que φ = 1.6180…

A Aplicação do Número de Ouro no Design

Por ser uma descrição matemática orgânica e que é repetida em vários elementos na natureza, visível desde a forma de crescimento de uma samambaia até na forma de uma galáxia, o número de ouro foi utilizado por várias escolas artísticas. Na arte grega e renascentista, o φ influenciou na arquitetura, na escultura e na pintura. Leonardo Da Vinci, em sua Gioconda, é um belo exemplo do uso da Espiral de Ouro nas proporções da Monalisa. Talvez um dos maiores exemplos do uso da Proporção Áurea seja o Homem Vitruviano, também de Da Vinci, onde este mostra as proporções perfeitas em um ser-humano.

Arte e matemática são ferramentas fundamentais do design moderno, o uso do número φ se torna fundamental para a criação de artefatos visuais cada vez mais orgânicos e esteticamente admiráveis. Mesmo quando não feito propositalmente, o ser-humano tende a buscar esse número ou uma aproximação do mesmo.

No design gráfico, a espiral de Fibonacci talvez seja a forma mais usada para criar uma leitura mais fluida dos elementos da imagem. Na diagramação de livros, por exemplo, o uso de retângulos áureos são usados para criar um espaçamento entre bordas mais confortáveis para a leitura.

Não diferente, o designer tende a utilizar uma razão mais próxima possível do retângulo áureo nas medidas dos papéis, as vezes, arredondando os lados para uma compreensão mais simples em produtos que exigem a medição do usuário ou específicas para determinadas máquinas. Todavia, optar por formatos padrões com proporção mais próximas ao retângulo áureo, ajuda a ter um resultado mais apropriado e orgânico.

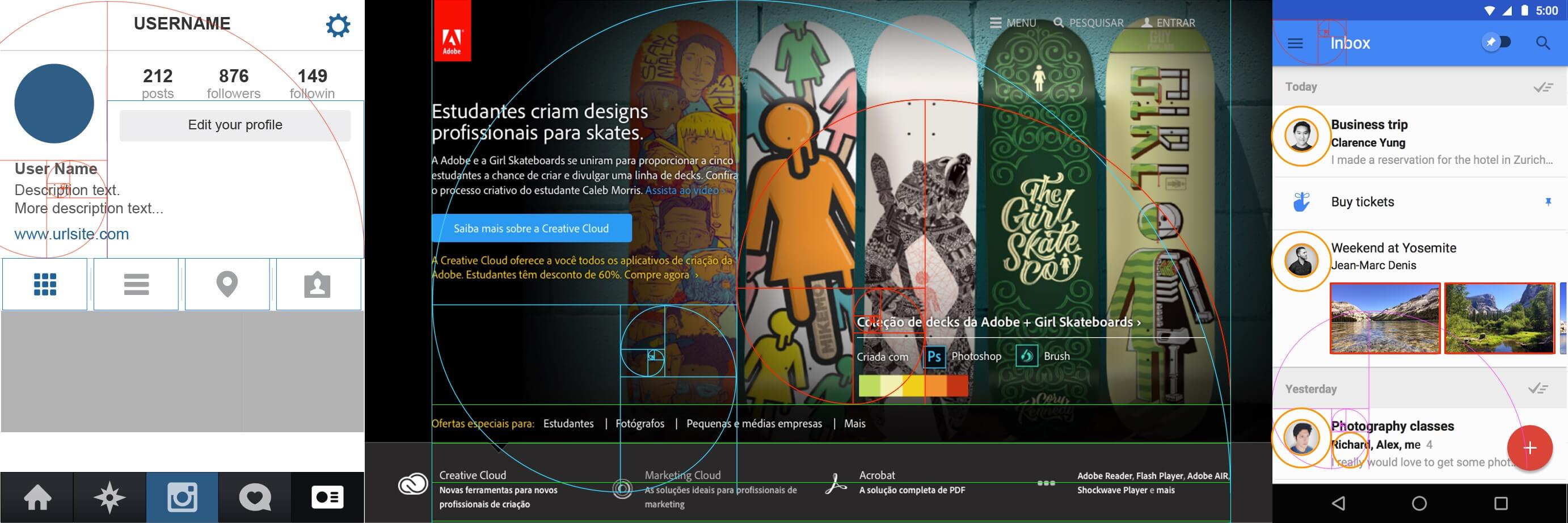
Qualquer artefato gráfico que exija uma melhor compreensão e objetividade na informação, como em revistas e interfaces gráficas para computadores, pode tirar um bom proveito da Proporção de Ouro e da Espiral de Fibonacci. Todos os produtos, ícones e marcas da Apple, por exemplo, são baseados na Espiral de Fibonacci.

Um dos motivos pelo qual a interface do iOS, da Apple, parecer mais bem acabada que a do que a de outros Sistemas Operacionais móveis, é a proporção com a qual seus ícones são criados. A Apple disponibiliza uma guideline para ícones. Essas linhas-guia são criadas a partir da referência da Espiral e Fibonacci. Na verdade,  os quadrados que formam a espiral são transformados em círculos e centralizados. A Proporção Áurea tem seu uso recorrente na área de iconografia.

A tipografia também é um estudo que utiliza as proporções áureas. Tanto a própria criação do tipo per si quanto a forma como ele é utilizado, a proporção áurea torna-se fundamental no planejamento. Para criar a tipografia, as Proporções Áureas são usadas para gerar suas formas.

Já no que diz respeito a utilização da tipografia aplicada em textos, podemos usar a proporção áurea para saber quais os diferentes tamanhos de tipos podemos usar em um artefato gráfico.

1em  2em   3em  5em 8em

O Número de Ouro é aplicável em qualquer cálculo matemático em que se busca uma proporção mais orgânica, é utilizável até mesmo em cores. O cálculo pode ser feito através de frequências ou calculando em números decimais por canal de cor. Já existem alguns aplicativos que tentam gerar essas cores baseadas em φ. Talvez a maneira mais eficiente seja calcular a paleta a partir de um Pentagrama Regular colocado em cima de um Disco Cromático de Newton.

Na área de Design de Interação, é comum achar cálculos que respeitem o Número de Ouro e a Proporção Áurea na preparação de interfaces. Apesar de ser um processo dependente de tecnologias e diversos outros fatores relacionados a websemântica, é possível gerar guias que usam proporções para encaixar melhor elementos na página.

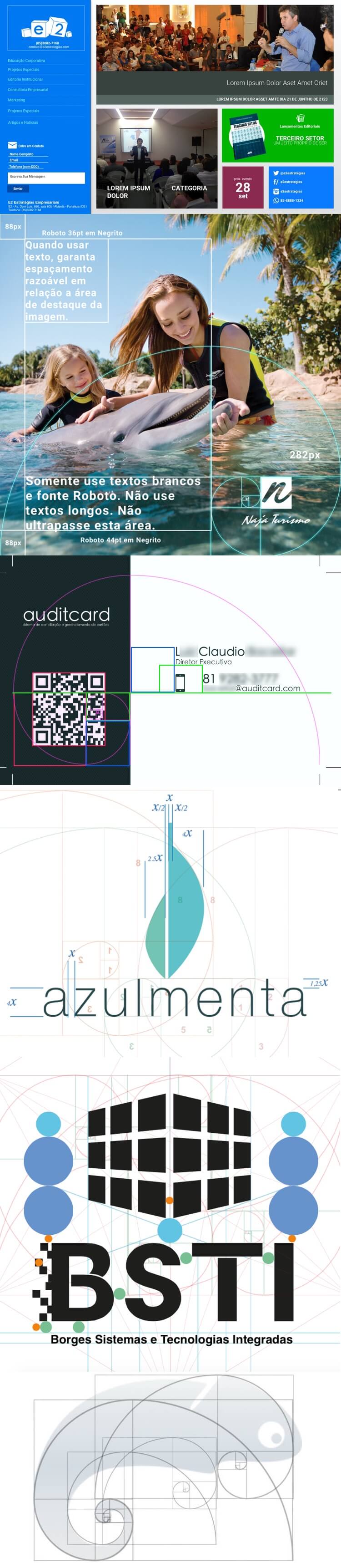
Todavia o local onde o Número de Ouro é mais é lembrado, na área de Design Gráfico, são nas Identidades Visuais.

Um designer gráfico geralmente cria o seu conceito no papel e quando vai finalizar sua marca, organiza suas curvas, espaçamentos e formas a seguir um padrão de grade que este cria. Esse padrão de grade, na maioria das vezes, é criado respeitando a Proporção Áurea e tende a ser seguido por todos os outros produtos e serviços relacionados à essa marca.

Além da grade, a Proporção φ também é usada para gerar objetos de tamanhos diferentes mas respeitando a composição, deixando a aparência final mais fluida. Mesmo sem querer, os designers são condicionados a finalizar suas criações usando essas proporções, com o tempo isso se torna quase automático. Todavia, é importante o uso das Proporções Áureas até mesmo para criar um conceito estético ou se o desejo for desconstruir completamente a proporção para chegar no conceito e função da forma que está sendo projetada.

Aqui mesmo na PortilloDesign, utiliamos Proporção Áurea e o Número de Ouro em alguns de nossos projetos.

Apesar da utilização do número de ouro ser importante em projetos gráficos, não significa que ele sempre deve ser sempre seguido à risca. Algumas vezes, dependendo do projeto, talvez o ideal seja não usar esses cálculos ou usar outras referências de grades. Todavia, para se quebrar uma regra, precisa primeiro conhece-la bem. Além disso, uso da proporção áurea não significa usar as formas redondas e retângulares que a ilustra, mas sim usar seus conceitos e cálculos para se chegar a uma forma ideal para o projeto. A proporção áurea é, como seu próprio nome diz uma referência de proporção e não exatamente da forma.

Concluindo

O Número de Ouro e a Proporção Áurea fazem parte de um conhecimento geométrico fundamental para o designer. A medida que os elementos naturais tendem a seguir a geometria fractal, simular esse efeito em seus projetos conduzem o designer a um acabamento mais agradável, tanto orgânico quanto esteticamente, aos olhos do observador. Além disso, a criação de grades baseadas nessas proporções ajuda como um estímulo à criatividade, definindo linhas e formas que podem ser transformadas na mente do criador.

Vale lembrar que nem sempre estamos fazendo algo pensando na proporção áurea ou definindo uma grade em todos os projetos. Com o tempo, essas definições acabam se tornando intuitivas e o designer acaba por adicionar essas formas mentalmente, sem nem mesmo perceber. Esse fenômeno explica o porquê de designers mais experientes conseguirem, muitas vezes, concluir projetos complexos em menos tempo.

Claro que, assim como os simulacros da computação gráfica, a adição de fatores aleatórios que quebram parte dessa proporcionalidade é algo muito bem-vindo, se usado com responsabilidade. O importante, em todo caso, é compreender como funcionam essas formas de desenvolvimento e a relação entre geometria, álgebra e geração de conteúdo usando essa tão desejada proporção 1.61, φ.